No discussion of geospatial analysis would be complete without a brief overview of basic statistical concepts. The statistics outlined here represent a starting point for any attempt to describe, summarize, and analyze geospatial datasets. An example of a common geospatial statistical endeavor is analyzing point data obtained by a series of rainfall gauges patterned throughout a particular region. Given these rain gauges, one could determine the typical amount and variability of rainfall at each station and regular rainfall throughout the region. In addition, a GIS analyst could interpolate the amount of precipitation that falls between each station or the location where the most (or least) rainfall occurs. Furthermore, the analyst could predict the expected amount of rain in the future at each station, between stations, or within the region.

Over the past few decades, the increase in computational power has given rise to vast datasets that cannot be summarized easily. Descriptive statistics provide simple numeric descriptions of these large datasets. Descriptive statistics are univariate analyses, meaning they examine one variable simultaneously. There are three families of descriptive statistics that we will discuss here: measures of distribution, measures of central tendency, and measures of dispersion. However, before we delve too deeply into various statistical techniques, we must first define a few terms.

• Variable: a symbol used to represent any given value or set of values
• Value: an individual observation of a variable (in a geographic information system [GIS], this is also called a record)
• Population: the universe of all possible values for a variable
• Sample: a subset of the population
• n: the number of observations for a variable
• Array: a sequence of observed measures (in a GIS, this is also called a field and is represented in an attribute table as a column)
• Sorted Array: an ordered, quantitative array

Measures of Distribution

The measure of distribution of a variable is merely a summary of the frequency of values over the range of the dataset (hence, this is often called a frequency distribution). Typically, the values for the given variable will be grouped into a predetermined series of classes (also called intervals, bins, or categories), and the number of data values that fall into each class will be summarized. A graph showing the number of data values within each class range is called a histogram. For example, the percentage of grades received by a class on an exam may result in the following array (n = 30):

Array of Exam Scores: {87, 76, 89, 90, 64, 67, 59, 79, 88, 74, 72, 99, 81, 77, 75, 86, 94, 66, 75, 74, 83, 100, 92, 75, 73, 70, 60, 80, 85, 57}

The following general guidelines should be observed when placing this array into a frequency distribution. First, five and fifteen different classes should be employed, although the exact number of classes depends on the number of observations. Second, each observation goes into one and only one class. Third, use classes that cover an equal range of values (Freund and Perles 2006). With these guidelines in mind, the exam score array shown earlier can be visualized with the following histogram.

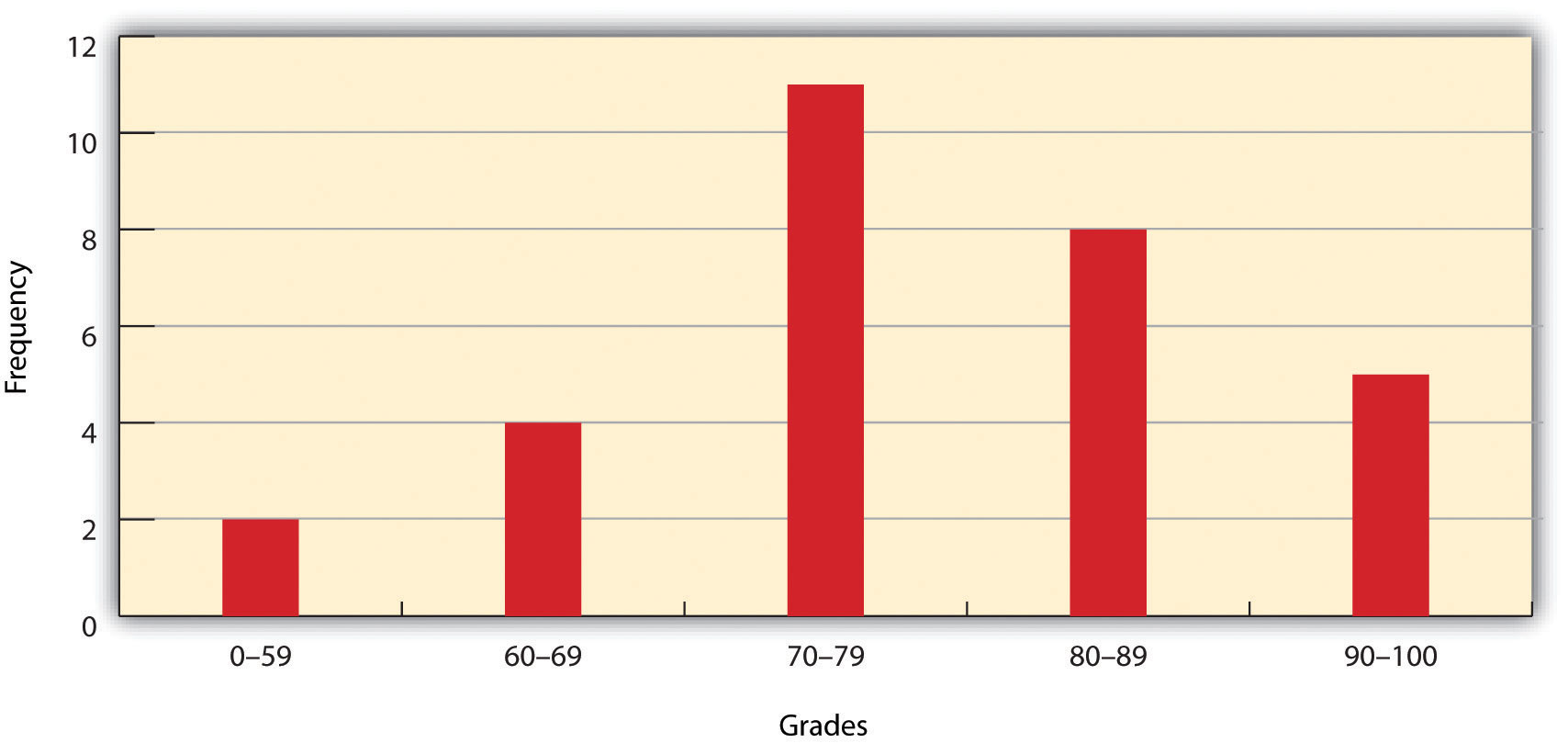
As shown from the histogram, specific descriptive observations can be readily made. Most students received a C on the exam (70–79). Two students failed the exam (50–59). Five students received an A (90–99). Note that this histogram does violate the third basic rule that each class covers an equal range because an F grade ranges from 0–59, whereas the other grades have ranges of equal size. Regardless, in this case, we are most concerned with describing the distribution of grades received during the exam. Therefore, creating class ranges that best suit our individual needs makes perfect sense.

Measures of Central Tendency

We can further explore the exam score array by applying measures of central tendency. There are three primary measures of central tendency: the mean, mode, and median. The mean, more commonly referred to as the average, is the most often used measure of central tendency. To calculate the mean, add all the values in the array, and divide that sum by the number of observations. To return to the exam score example from earlier, the sum of that array is 2,340, and there are 30 observations (n = 30). So, the mean is 2,340 / 30 = 78.

The mode measures central tendency representing the most frequently occurring value in the array. For example, in the case of the exam scores, the mode of the array is 75, as this was received by most students (three in total). Finally, the median is the observation that, when the array is ordered from lowest to highest, it falls precisely in the center of the sorted array. More specifically, the median is the value in the middle of the sorted array when there are an odd number of observations. Alternatively, when there is an even number of observations, the median is calculated by finding the mean of the two central values. For example, if the array of exam scores were reordered into a sorted array, the scores would be listed this way:

Sorted Array of Exam Scores: {57, 59, 60, 64, 66, 67, 70, 72, 73, 74, 74, 75, 75, 75, 76, 77, 79, 80, 81, 83, 85, 86, 87, 88, 89, 90, 92, 93, 94, 99}

Since n = 30 in this example, there are an even number of observations. Therefore, the mean of the two central values (15th = 76 and 16th = 77) is used to calculate the median as described earlier, resulting in (76 + 77) / 2 = 76.5. The mean, mode, and median represent the most basic ways to examine trends in a dataset.

Measures of Dispersion

The third type of descriptive statistics is measures of dispersion (also referred to as measures of variability). These measures describe the spread of data around the mean. The most straightforward measure of dispersion is the range. The range equals the most significant value minus in the dataset the smallest. In our case, the range is 99 − 57 = 42.

The interquartile range represents a slightly more sophisticated measure of dispersion. This method divides the data into quartiles. The median is used to divide the sorted array into two halves. These halves are again divided into halves by their median. The first quartile (Q1) is the median of the lower half of the sorted array and is also referred to as the lower quartile. Q2 represents the median. Q3 is the median of the upper half of the sorted array and is referred to as the upper quartile. The difference between the upper and lower quartile is the interquartile range. In the exam score example, Q1 = 72.25 and Q3 = 86.75. Therefore, the interquartile range for this dataset is 86.75 − 72.25 = 14.50.

The third measure of dispersion is the variance (s2). To calculate the variance, subtract the raw value of each exam score from the mean of the exam scores. Some differences will be positive, and some will be negative, resulting in the sum of differences equaling zero. As we are more interested in the magnitude of differences (or deviations) from the mean, one method to overcome this “zeroing” property is to square each deviation, thus removing the negative values from the output. This results in the following:

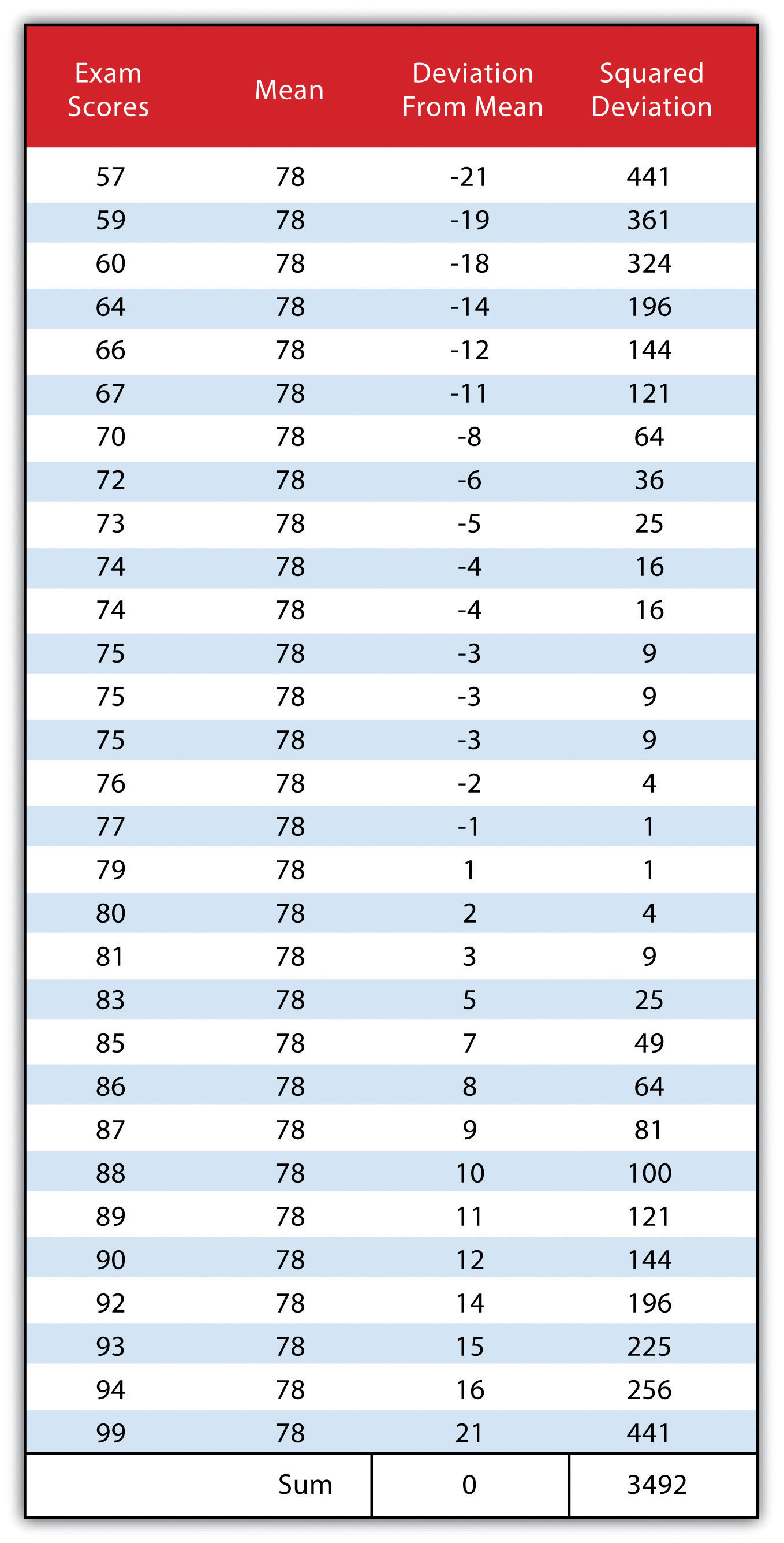
We then divide the sum of squares by either n -1 (in the case of working with a sample) or n (in the case of working with a population). As the exam scores here represent the entire class population, we will employ this figure on variance, resulting in a variance of s2 = 116.4. However, we would be working with a population sample if we wanted to use these exam scores to extrapolate information about the larger student body. In that case, we would divide the sum of squares by n − 1.

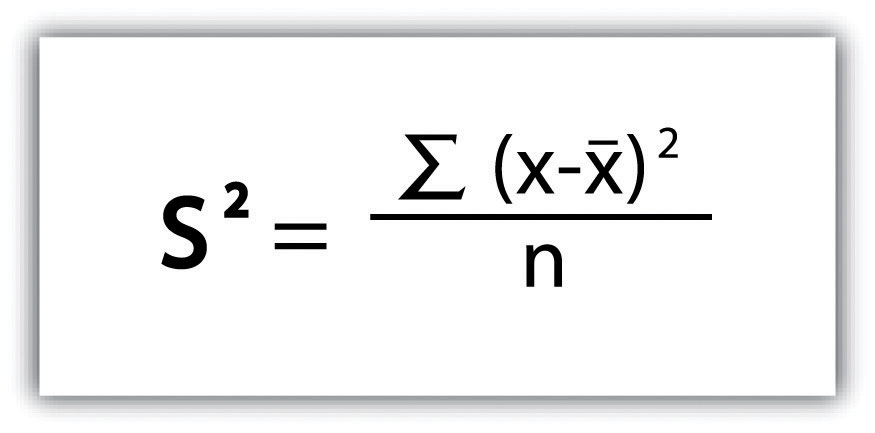
Standard deviation, the final measure of dispersion discussed here, is the most commonly used measure of dispersion. To compensate for the squaring of each difference from the mean performed during the variance calculation, standard deviation takes the square root of the variance. As determined from the figure on standard deviation, our exam score example shows a standard deviation of s = SQRT(116.4) = 10.8.

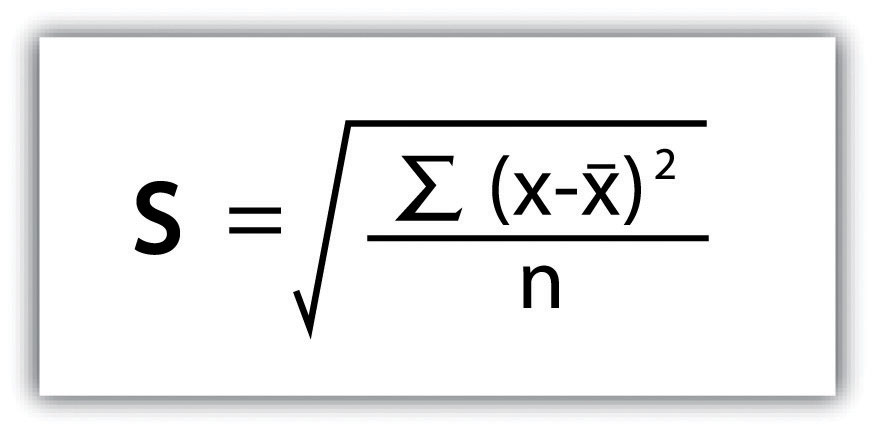
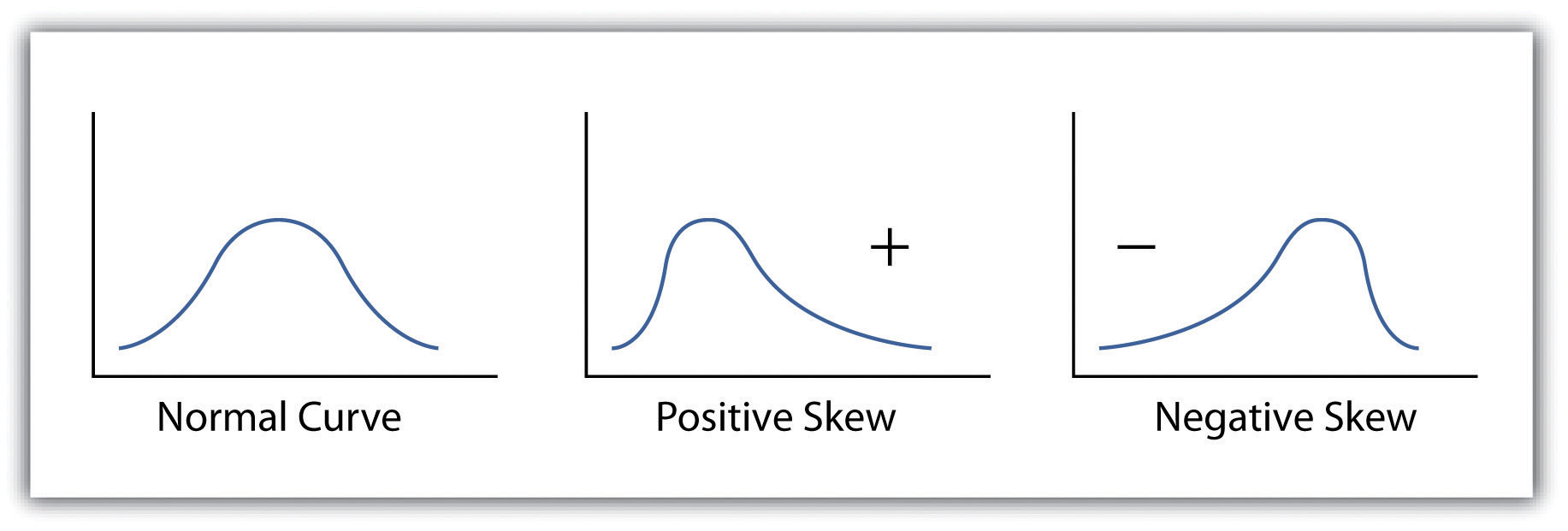
Calculating the standard deviation allows us to make some notable inferences about the dispersion of our dataset. A slight standard deviation suggests the values in the dataset are clustered around the mean, while a significant standard deviation indicates the values are scattered widely around the mean. Additional inferences about the standard deviation may be made if the dataset conforms to a normal distribution. When placed into a frequency distribution (histogram), a normal distribution implies that the data looks symmetrical or “bell-shaped.” When not “normal,” the frequency distribution of the dataset is said to be positively or negatively skewed. Skewed data maintain values that are not symmetrical around the mean. Regardless, normally distributed data supports the property of having approximately 68 percent of the data values fall within ±1 standard deviation of the mean, and 95 percent of the data value fall within ±2 standard deviations of the mean. In our example, the mean is 78, and the standard deviation is 10.8. It can therefore be stated that 68 percent of the scores fall between 67.2 and 88.8 (i.e., 78 ± 10.8), while 95 percent of the scores fall between 56.4 and 99.6 (i.e., 78 ± [10.8 * 2]). For datasets that do not conform to the standard curve, it can be assumed that 75 percent of the data values fall within ±2 standard deviations of the mean.

Click the “Previous” button on the lower left or the ‘Next” button on the lower right to navigate throughout the textbook.