23 Lab Protocol: Genetics

Investigating the importance of a large data set using a pair of coins

Collect data sets to analyze:

1. Each group of students will collaborate to propose a hypothesis to predict the possible outcomes and their frequencies when flipping a pair of pennies. Record in row 1 of data table below (expected percentages).

1. Each student will flip a pair of pennies 10 times and record their results as a percentage in data table row 2.

1. Each student will repeat step 2 three more times recording their results each time (rows 3 – 5).

1. Calculate the average percentages for rows 2 – 5 and record in row 6. This represents the results for a data set of 40.

1. Calculate the average of row 6 for all group members and record in row 7. This represents the results of a data set of 120 or 160.

1. Calculate the average of row 6 for all class members and record in row 8.  This represents the results of a data set of 800 – 1000.

1. Groups will analyze the experimental results to determine if their original hypothesis might reasonably explain the data collected. If not, propose a new hypothesis (row 9).

Analyze data to investigate the impact of set size:

1. Use the percentages indicated in row 9 in the table above as the expected percentages. Subtract the observed frequency from the expected frequency for each category (2 heads, 1 head/1 tail, and 2 tails) and record positive difference in proper column. The table should not have any negative numbers in it.

1. Calculate the total difference for each row by adding up the three differences (2 heads + 1 head/1 tail + 2 tails) and record in final column of table.

1. Compare the total deviations (final column of table) and arrange in order from smallest number to largest number.  Record results by listing the size of the data set separated by commas.  Example: 10, 160, 1000, 10, 40, 10, 10

1. Write a general conclusion to describe the relationship between total deviation and size of data set.

Phenotype ratios associated with the parental, F1, and F2 generations of a dihybrid cross

It would require at least a year to grow three sequential generations of corn plants.  We will therefore not grow or cross corn plants in this lab, but we will analyze purchased corn cobs produced by someone else. We will analyze two different segregating characteristics: purple versus yellow color, and smooth versus wrinkled kernels. Whenever you are asked to describe phenotypes, choose from the following four possibilities: purple smooth, yellow smooth, purple wrinkled, and yellow wrinkled.  Keep in mind that true-breeding individuals will be homozygous for the genes involved.

1. What phenotype(s) is/are associated with the two true-breeding parental cobs? Also indicate the frequency of each.

1. Parent cob 1:

1. Parent cob 2:

1. Can we determine if purple is dominant over yellow or if smooth is dominant over wrinkled by looking at the parental cobs? Explain.

1. What phenotype(s) is/are associated with the F1 cob? Also indicate the frequency of each phenotype:

1. Which is the dominant phenotype?

1. Purple or yellow?

1. Smooth or wrinkled?

1. Write a legend to assign names to the genes and the alleles associated with the corn kernels.

1. Indicate the genotypes of both parents and of the F1 generation.

1. Indicate the genotypes of another set of true-breeding parents that could also produce dihybrid F1 offspring.

1. Draw a Punnett square describing a cross between two F1 individuals.  Be sure to display the gamete types produced by each parent and the genotypes of the F2 offspring in their proper locations.

1. Add offspring phenotypes to the Punnett square.

1. Based on the Punnett square, fill in the second and third columns of the data table.

1.  Count the kernels of the F2 generation cobs according to their phenotypes and place in the 4th column of the data table. Randomly count at least 100 kernels.

1.  Calculate the frequency of each kernel type as a percentage and place into 5th column.

1.  Speculate why the percentages in column 3 might not be the same as in column 5.

Using a Pedigree chart to predict the likelihood that a particular child will be colorblind, an X-linked recessive trait

Analyze the following pedigree chart that displays the inheritance of colorblindness.

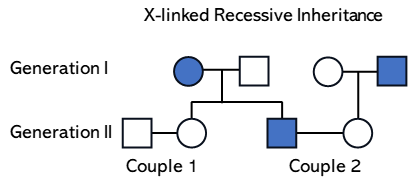
1. Write a legend to describe the allele symbols you will use.

1. Indicate all that you can about the genotype of each individual without analyzing any relationships between individuals.

1. Now look at relationships to complete each genotype. List both genotypes if two different genotypes are possible for any individual.

1. Use a Punnett square to predict the probability of colorblindness.

1. First daughter of couple 1:

1. First son of couple 1:

1. First daughter of couple 2:

1. First son of couple 2:

Analysis of human blood type

Sometimes a geneticist is asked to use the phenotypes of family members to predict their genotypes. One example of this is using the phenotypes of children to determine the genotypes of the parents.  A good way to do this is to construct a Punnett square placing the phenotypes of the children in the offspring squares and working backwards to predict gamete types for each parent. These gamete types can then be used to determine the genotype of each parent.

1. Story problem 1: Father has type A+ blood and mother has type B- blood.  The couple has six children with the following phenotypes: AB+, A-, AB+, A+, A+, AB+. What are the genotypes of the parents assuming that additional children would not introduce other blood types.

1. Story problem 2: In a paternity case, the mother has blood type O-. What are the possible phenotypes of the father if the child has blood type A+.

1. Design and carry out an experiment to determine the blood types of 4 different individuals. Use controls of known blood type as you plan and carry out your analysis.